Mathematical Relationships in Science

---

What is a Mathmatical Relation?

A mathematical relation is, a relationship between sets of numbers or sets of elements.

Often you can see relationships between variables by simply examining a mathematical equation. Many physical relationships in electrostatics, electrodynamics, thermodynamics, etc. are expressed by mathematical equations. The following examples for mathematical relationships will help you in analyzing data for the labs in this module.

Linear Relationships

Let's look at the following equation:

Y = 3X

As X increases Y will increase proportionally. If we plot the X-y graph a straight line will be formed.

In nature data is not exact so points will not always fall on the line. Below is a graph of data relating Specific Crushing Strength with Pressure (P). The points fall close enough to the straight line to conclude that this is a linear or direct relationship.

 

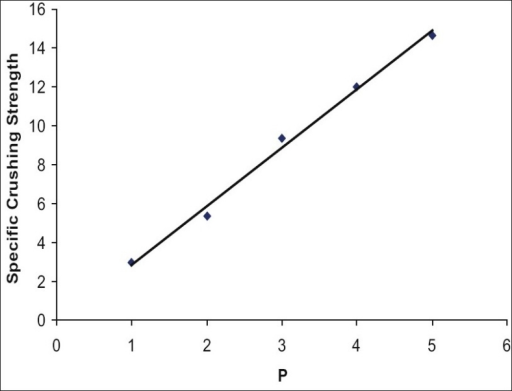
What are independent and dependent variables in the graph?

Independent variable -An independent variable is exactly what it sounds like. It is a variable that stands alone and isn't changed by the other variables you are trying to measure. For example If time is one of your variables, it is the independent variable. Time is always the independent variable. Scientists like to say that the "independent"variable goes on the x-axis (the bottom, horizontal one) and the "dependent" variable goes of the y-axis (the left side, vertical one).

Dependent variable -- Just like an independent variable, a dependent variable is exactly what it sounds like. It is something that depends on other factors. For example, a test score could be a dependent variable because it could change depending on several factors such as how much you studied, how much sleep you got the night before you took the test, or even how hungry you were when you took it. Usually when you are looking for a relationship between two things you are trying to find out what makes the dependent variable change the way it does.

Inverse Relationship

Now, let's look at the following equation:

Y = 1/X

If X=1 then Y = 1. If X = 2, then Y = 0.5. If X = 3 then Y = 0.33. If X = 4, then Y = 0.25. Note that as X increases Y decreases in a non-linear fashion. This is an inverse relationship.

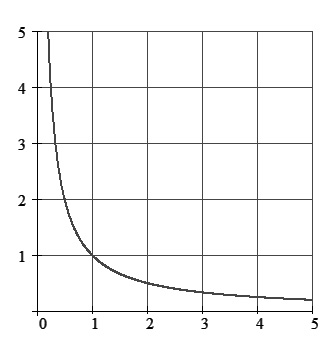
Example of an inverse relationship in science: When a higher viscosity leads to a decreased flow rate, the relationship between viscosity and flow rate is inverse. Inverse relationships follow a hyperbolic pattern. Below is a graph that shows the hyperbolic shape of an inverse relationship.

 

Quadratic Relationship

A quadratic relationship between x and y means y is related to x^2 , x and a constant (C) by a function, which generally represented as: y = A x^2 + B x + where A must be a non-zero number.

Quadratic formulas are often used to calculate the height of falling rocks, shooting projectiles or kicked balls. A quadratic formula is sometimes called a second degree formula.

The simplest type of quadratic equation is y = x^2

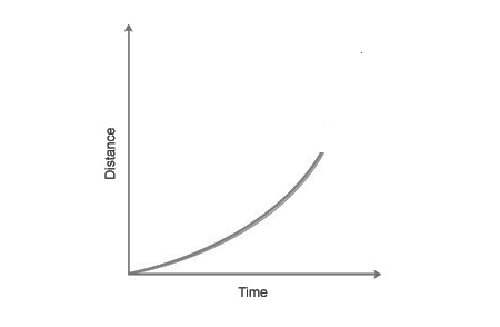
Examples: Quadratic relationships are found in all accelerating objects e.g., falling objects. Below is a graph that demostrates the shape of a quadratic equation.

 

Inverse Square Law

The principle in physics that the effect of certain forces, such as light, sound, and gravity, on an object varies by the inverse square of the distance between the object and the source of the force. For example, an object placed three feet away from a light source will receive only one ninth ( 1/9 , the inverse of 3 squared) as much illumination as an object placed one foot from the light.

 

In physics, an inverse-square law is any physical law stating that a specified physical quantity or intensity is inversely proportional to the square of the distance from the source of that physical quantity. The fundamental cause for this can be understood as geometric dilution corresponding to point-source radiation into three-dimensional space.

One of the famous inverse square laws relates to the attraction of two masses. Two masses at a given distance place equal and opposite forces of attraction on one another. The magnitude of this force of attraction is given by:

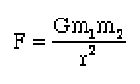
where G is the universal gravitation constant (6.67 X 10-11 Nm2/kg^2), m1 is the mass of the first object in kilograms, m2 is the mass of the second object in kilograms, and r is the distance between the centers of the two masses, in meters. The graph of this equation is shown below.

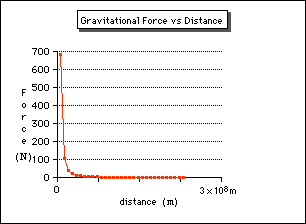
Gravity:Another example of a 1/R2 Law (image from NASA)

Damping Motion

Damping is an influence within or upon an oscillatory system that has the effect of reducing, restricting or preventing its oscillations. In physical systems, damping is produced by processes that dissipate the energy stored in the oscillation. Examples include viscous drag in mechanical systems, resistance in electronic oscillators, and absorption and scattering of light in optical oscillators. Damping not based on energy loss can be important in other oscillating systems such as those that occur in biological systems.

 

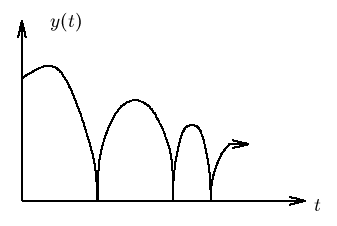
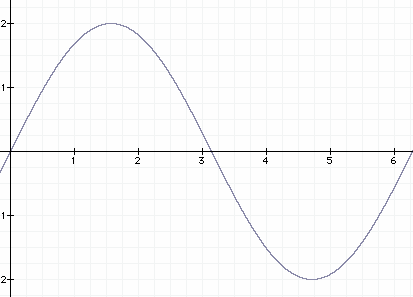
Sine Wave Relationship

The graphs of the sine and cosine functions are sinusoids of different phases. The sine wave or sinusoid is a mathematical curve that describes a smooth repetitive oscillation. It is named after the function sine, of which it is the graph.